"

Ch. 7 Time Value of Money and Valuations

7.4 Present Value

Learning Objective

Once you complete this section, you will be able to:

  • Calculate the present value of both single future payments and multiple periodic payments using appropriate formulas and Excel tools, accounting for different compounding frequencies.

While future value analysis tells us what an investment will grow to in the future, present value (PV) helps us determine what a future amount is worth today. In other words, present value answers the question: How much should I invest today to receive a specific amount in the future, assuming a particular interest rate? This concept applies both to a single future payment and to a series of periodic payments (annuities). We begin with the present value of a single amount.

PRESENT VALUE OF SINGLE AMOUNTS

Present value is grounded in the fundamental idea that a dollar received today is worth more than a dollar received later, because today’s dollar can be invested to earn interest. Here are common situations where an attorney would use present value (PV) single amount calculations in legal practice:

  • Evaluating Lump-Sum Settlements: When comparing a lump-sum settlement offered today with a larger future payment or trial award, attorneys use present value (PV) to determine which option is financially more favorable.
  • Estate and Trust Planning: To plan distributions, attorneys calculate the PV of a future bequest or gift to determine how much needs to be set aside today to fulfill a future obligation or charitable promise.
  •  Structured Payment Agreements: In business or personal contracts, lawyers may use PV to value future balloon payments or final lump-sum payments promised at the end of an installment plan or lease.
  • Deferred Compensation and Employment Contracts: Employment attorneys use PV to assess the current value of deferred bonuses or severance packages payable in the future, aiding in negotiations and tax planning.
  • Prejudgment Interest Calculations: In litigation, attorneys may calculate the PV of a future damages award when arguing for or against prejudgment interest, especially in jurisdictions without a fixed statutory rate.
  • Funding Education or Special Needs Trusts: When setting up a trust to meet a specific future expense (e.g., tuition or major medical cost), attorneys calculate how much must be invested today to reach the needed amount on time.
  • Buy-Sell Agreements and Business Valuation: In corporate law, attorneys may evaluate the present value of future payments under a buy-sell agreement or when calculating equity buyouts between partners.
  • Divorce and Property Division: In family law, attorneys sometimes determine the PV of a future lump-sum payment (e.g., from a pension or business interest) to ensure fair marital asset distribution.

Suppose someone offers to pay you $1,050 one year from now. If the interest rate is 5%, how much is that promise worth today?

Using the formula:

PV = FV/ (1+r)^n  =  $1,050/(1+0.05)^1  =  $1,000

Where:

  • PV = Present Value
  • FV = Future Value
  • r = annual interest rate (as a decimal)
  • n = number of compounding periods per year

This means the present value of $1,050 a year from now, at 5% interest, is $1,000.

Example: Education Fund Promise

Sophia promises to give her niece $15,000 when she turns 21, which will be in 8 years. What is the present value of that promise if we use a 6% annual discount rate?

Using a present value factor:

PV = FV/(1+r)^n = $15,000/(1+0.06)^8 = $9,411.19

So, the promise to pay $15,000 in 8 years is worth about $9,411 today.

This can also be verified in Excel. You can use the PV function:

=PV(0.06, 8, 0, -15000)

This will return approximately $9,411.19, representing the present value of the $15,000 future payment.

 

 

Attorneys use present value single amount calculations in various legal contexts to evaluate the current worth of future payments.

Now consider what happens if the interest is compounded more frequently than annually.

Example: Education Fund Promise with Semi-annual Compounding

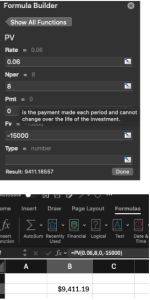
Sophia promises to give her niece $15,000 when she turns 21, which will be in 8 years and interest is compounded semiannually instead of annually. In this case, you divide the interest rate and double the number of periods:

  • Rate per period = 6% ÷ 2 = 3% = 0.03
  • Total periods = 8 × 2 = 16

Use the adjusted formula:

PV = FV/(1+r/2)^n*2 = $15,000/(1+0.06/2)^8*2 = $9,347.50

So, the promise to pay $15,000 in 8 years, compounding semi-annually, is worth about $9,347.50 today. With more frequent compounding, the present value is slightly lower because the money would earn interest more often if invested today.

You can calculate this in Excel with:

=PV(0.03, 16, 0, -15000)

 

 

 

PRESENT VALUE OF MULTIPLE AMOUNTS

Here are common situations where an attorney would use present value (PV) of annuities (i.e., multiple amounts that are the same) in practice:

  • Charitable Endowments: Attorneys advising donors on endowing fellowships, scholarships, or chairs calculate the present value of an annuity to determine the necessary gift amount, factoring in inflation-based annual increases.
  • Family Foundations or Legacy Trusts:  When setting up long-term family trusts with inflation-adjusted annual disbursements, lawyers use the PV of an annuity to plan the initial contribution needed to sustain the payouts.
  •  Corporate Governance and Nonprofit Funding: Attorneys representing universities, hospitals, or nonprofit boards may calculate how much a permanent funding source must contribute today to generate an income stream for operations.
  • Long-Term Royalty or Licensing Agreements:  If a client receives royalty payments over time (e.g., tied to inflation), attorneys use the present value of an annuity to assess buyouts or asset transfers.

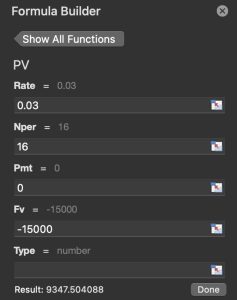
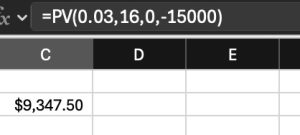
Suppose someone offers to pay you $1,050 per year for 5 years, with the first payment one year from now. If the annual interest rate is 5%, how much are those five payments worth today?

Using the present value of an ordinary annuity formula:

PV = PMT × ((1−(1+r)−n)/r) 

Where:

  • PV = Present Value
  • PMT = Annual payment
  • r = Annual interest rate
  • n = Number of years

Using the example above, the calculation would be:

PV = $1,050×(1−(1+0.05)−5/0.05) = $1,050×4.32948 = $4,545.95

The present value of receiving $1,050 annually for 5 years, at a 5% interest rate, is approximately $4,545.95. This reflects the total worth today of the anticipated future payments.

In Excel, the formula function would show the following fields:

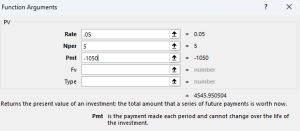
Example: Present Value of an Annuity in a Structured Settlement

An attorney represents a client in a personal injury case. The defendant offers to settle by paying the client $50,000 annually for 10 years, rather than offering a lump-sum payment today. The attorney wants to evaluate the present value of those payments to determine whether the structured settlement is financially fair. The appropriate discount rate (interest rate) is 4%, based on current market conditions.

Using the present value formula:

PV = PMT × ((1−(1+r)−n)/r) 

Where:

  • PMT = $50,000 (annual payment)

  • r = 0.04 (annual discount rate)

  • n = 10 years

In Excel, the calculation would look as follows:

=PV(0.04, 10, 0, -50000)

 

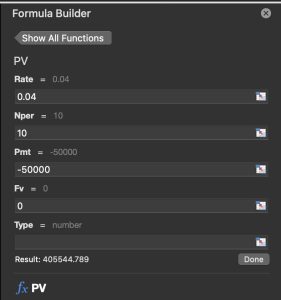
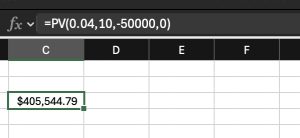
The present value of the 10-year annuity at a 4% discount rate is approximately $405,545. This tells the attorney that if the client were to receive a lump sum today, a fair amount would be around $405,545, allowing the client to make an informed decision about accepting the structured settlement or negotiating for a larger upfront payment.

 

PERPETUAL ANNUITIES

So far, we’ve examined annuities with a set duration. However, a perpetual annuity (or perpetuity) is structured to continue indefinitely. Because the original principal must remain untouched, the investor may only withdraw the interest earned each period to ensure the payments last forever. The equation to calculate the perpetuity is: 

PV = Annual Payment/Interest Rate

Example: Retirement Planning with a Perpetuity

Jordan is preparing for retirement and wants to receive $75,000 annually for the rest of his life, leaving the principal intact to provide the same payments to his heirs. If he expects a 5% annual return, how much does he need to invest?

Using the formula for the present value of a perpetuity:

PV = Annual Payment/Interest Rate =

$75,000/(0.05) = $1,500,000

In Excel, the calculation is shown as:

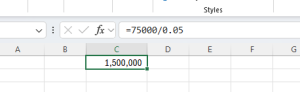
Jordan would need to invest $1.5 million at 5% to receive $75,000 per year indefinitely.

 

In some cases, a perpetual annuity grows over time (e.g.,  to match inflation). The present value of a perpetuity that grows at a constant rate is calculated as follows:

PV = Payment/ (Interest Rate – Growth Rate)

Example: Endowed Legal Fellowship

Attorney Maya wants to endow a legal fellowship at her alma mater that pays $50,000 per year and increases 3% annually to keep pace with inflation. If the law school’s investment fund is expected to earn 7% annually, how much must Maya contribute?

PV = Payment/ (Interest Rate – Growth Rate) =

$50,000/(0.07-0.03) = 50,000/(0.04) = $1,250,000

In Excel, the calculation would be:

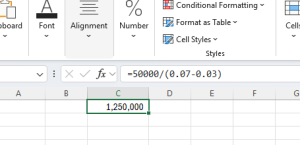
Maya must donate $1.25 million to fund the growing annual fellowship in perpetuity.

 

Understanding perpetuities is critical when advising clients on charitable trusts, permanent endowments, and other instruments designed to provide ongoing financial support. Lawyers can apply these principles in estate planning, nonprofit governance, and structured settlement design.

Homework 7.4.1

Scenario: Charitable Endowment for Legal Aid Fund

Attorney Singh represents a philanthropist who wants to establish a perpetual legal aid fund that will provide $100,000 per year indefinitely to support pro bono representation for low-income clients. The foundation’s investment account is expected to earn a 6% annual return, but the client wants payments to increase by 2% annually to offset inflation.

Requirements:
1) Calculate how much must be contributed today to fully fund the endowment.

Homework 7.4.2

Scenario: Structured Settlement Evaluation

In a personal injury case, the insurance company offers to pay $120,000 per year for 8 years, with the first payment one year from now, as a structured settlement instead of a single upfront payment. The appropriate discount rate is 5%, reflecting the current market return on comparable investments.

1) Calculate the present value of the 8 annual payments.

2) If the defendant instead offered a lump-sum payment today, what minimum amount would make the client financially indifferent between the two options?

Homework 7.4.3

Scenario: Lump-Sum Settlement Decision

Attorney Lopez is advising a client who won a breach-of-contract lawsuit. The defendant offers two settlement options:

  1. Receive $500,000 today, or

  2. Receive $540,000 one year from now.

The applicable discount rate is 6% per year, compounded annually.

Requirements:
1) Calculate the present value of the $540,000 future payment.
2) Determine which option is financially more favorable for the client.

 

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Accounting for Lawyers Copyright © 2024 by JoAnn Wood is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book