Analysis of Qualitative Data

Descriptive Statistics and Inferential Statistics.

Let’s say our sample is golden retrievers (population “canines”). Our descriptive statistics tell us more about the same.

• 37% of our sample is male, 43% female
• The mean age is 4 years
• Mode is 6 years
• Median age is 5.5 years

Types of descriptive statistics

Frequency Distributions: A frequency distribution describes the number of observations for each possible value of a measured variable. The numbers are arranged from lowest to highest and feature a count of how many times each value occurred.

For example, if 18 students have pet dogs, dog ownership has a frequency of 18.

We might see what other types of pets that students have. Maybe cats, fish, and hamsters. We find that 2 students have hamsters, 9 have fish, 1 has a cat.

You can see that it is very difficult to interpret the various pets into any meaningful interpretation, yes?

Central Tendency: A measure of central tendency is a single value that attempts to describe a set of data by identifying the central position within that set of data.

• Mode: The mode is the number that occurs most frequently in a distribution of values.
  • Example: 23 45 45 45 51 51 57 61 98
  • Mode: 45
• Median: The median is the point in a distribution of values that divides the scores in half.
  • Example: 2 2 3 3 4 5 6 7 8 9
  • Median: 4.5
• Mean: The mean equals the sum of all the values in a distribution, and then divided by the number of values.
  • Example: 85 109 120 135 158 177 181 195
  • Mean: 145

Now, in a normal distribution of data, the values are symmetrically distributed. Meaning, most values cluster around a central region. It has a normal “Bell Curve”. Remember the frequency distribution from above? We see in this histogram that it has a normal distribution.

But what if it is not bell-shaped?

Well, that would be called a skewed distribution. The image below illustrates the differences between a Positive Skew, a Symmetrical Distribution, and a Negative Skew. A long description is provided below the image.

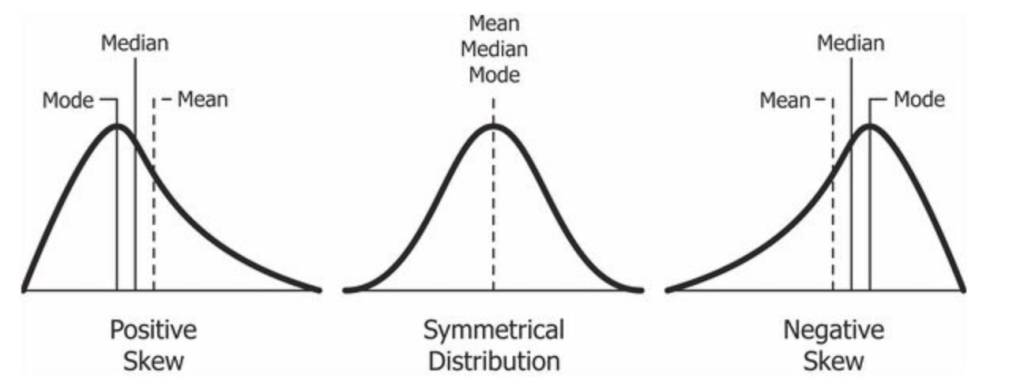
Image attribution: Relationship Between Mean and Median Under Different Skewness by Diva Jain from Wikimedia Commons is licensed CC BY-SA

Skew is usually bad. Remember that. A skewed distribution is also called asymmetric or asymmetrical distribution, as it does not show any kind of symmetry. Symmetry would mean that one half of the distribution is mirror image of the other half. If the distribution is skewed, it tells us that something is “off” and our statistical analysis might be difficult because errors are no longer distributed symmetrically around the mean (average) of the data. There are issues that will depend on specific features of the data and analytic approach, but in general, skewed data (in either direction) will degrade some of the ability to describe more “typical” cases in order to deal with much rarer cases which happen to take extreme values.

Variability

While the central tendency tells you where most of the data points lie, variability summarizes how far apart they are. This is really important because the amount of variability determines how well the researcher can generalize results from the sample to the population.

Having a low variability is ideal. This is because a researcher can better predict information about the population based on the data from the sample. Having a high variability means that the values of the data are less consistent. Thus, higher variability means it is harder to make predictions.

A normal distribution is defined by its mean and the standard deviation. The standard deviation is how much the data differs from its mean, on average.

Let’s look at that another way. Any normal collection of values will simply tend to cluster toward the mean, yes? If we have a homogenous (similar) sample or precise inclusion criteria for the sample, the data will probably not have huge variations. The standard deviation (SD) tells us the degree of clustering related to the average (mean). The SD summarizes the average amount of deviation of values from the mean. We want this fairly small, and the standardized value of the SD is usually around 2-3 SDs. If values fall outside of the standard deviation, this may mean there is an error in a collected value somewhere or that something is “off”. An SD can be interpreted as the degree of error when the mean is used to describe an entire sample.

Correlation

Relationships between two research variables are called correlations. Remember, a correlation is not cause-and-effect. Correlations simply measure the extent of the relationship between two variables.

To measure correlation in descriptive statistics, the statistical analysis called Pearson’s correlation coefficient is often used.  You do not need to know how to calculate this for this course. But, do remember that analysis test because you will often see this in published research articles. There really are no set guidelines on what measurement constitutes a “strong” or “weak” correlation, as it really depends on the variables being measured.

However, possible values for correlation coefficients range from -1.00 through .00 to +1.00. A value of +1 means that the two variables are positively correlated, as one variable goes up, the other goes up. A value of r = 0 means that the two variables are not linearly related.

Often, the data will be presented on a scatter plot. Here, we can view the data and there appears to be a straight line (linear) trend between height and weight. The association (or correlation) is positive. That means, that there is a weight increase with height. The Pearson correlation coefficient in this case was r = 0.56.

Inferential Statistics

When thinking of research in general, and how researchers can make inferences from their sample population and generalize it to the general population we are referring to inferential statistics. We are making inferences, or predictions, based on probabilities.

Inferential statistics are used to test research hypotheses.

Lucky for you, we will not explore all of the inferential statistical tests via analyses that can be done. However, we need to look at a couple of general key concepts.

Hypothesis testing

The key concept about testing a hypothesis, is that researchers are using completely objective criteria to decide whether the hypothesis should be accepted or rejected. That is, it is either supported with statistical evidence or it is found to not be supported.

Suppose we hypothesize that diabetic patients who received online interactive diabetic diet education would have better control of their blood sugar levels measured by 2-hour postprandial blood glucose than those who did not. The mean 2-hour postprandial blood glucose for the intervention group is 165 for 25 intervention diabetics and 186 for control group diabetics. Should we conclude that our hypothesis has been supported? Group differences are in the predicted direction, but in another sample, the group means might be more similar. Two explanations for the observed outcomes are possible: (1) The intervention was effective in educating diabetics or (2) the mean difference in this sample was due to chance (sampling error).

In the first explanation of an effective educational program, that is considered the research hypothesis. The second explanation is the null hypothesis, which means that there is no relationship between the independent variable (our intervention of online interactive diet education) and the dependent variable (our outcome of better control of postprandial blood glucose).

Now, remember, our hypothesis testing is a process of only supporting the prediction. There is no way to fully demonstrate that the research hypothesis is directly correct. However, it is possible to show that the null hypothesis has a pretty high probability of being incorrect – meaning, if we can show that something did happen, then we may be able to reject the null hypothesis and state that there is evidence to support the hypothesis.

Hypothesis testing simply allows researchers to make objective decisions about whether measured results happened because of chance, or if the results were actually because of hypothesized effects. That is key! Remember that last statement.

Type I and Type II Errors

The next step in understanding hypothesis testing is learning about Type I and Type II errors. Researcher have to decide (with the help of statistical analysis of their data) whether or accept or reject the null hypothesis. Back to the statement above that I told you to remember – researchers have to estimate how probable it is that the group differences are just due to chance. At the end of the day, researchers can only state that their hypothesis is probably true or probably false.

In making this decision, researchers can make errors. These errors can be that their reject an actual true null hypothesis, or that they accept a non-true (false) null hypothesis.

A type I error is made by rejecting a null hypothesis that is true. This means that there was no difference but the researcher concluded that the hypothesis was true.

A type II error is made by accepting that the null hypothesis is true when, in fact, it was false. Meaning there was actually a difference but the researcher did not think their hypothesis was supported.

Hypothesis testing procedures

In a general sense, the overall testing of a hypothesis has a systematic methodology. Remember, a hypothesis is an educated guess about the outcome. If we guess wrong, we might set up the tests incorrectly and might get results that are invalid. Sometimes, this is super difficult to get right. The main purpose of statistics is to test a hypothesis.

1. Selecting a statistical test. Lots of factors go into this, including levels of measurement of the variables.
2. Specifying the level of significance. Usually 0.05 is chosen.
3. Computing a test statistic. Lots of software programs to help with this.
4. Determining degrees of freedom (df). This refers to the number of observations free to vary about a parameter. Computing this is easy (but you don’t need to know how for this course).
5. Comparing the test statistic to a theoretical value. Theoretical values exist for all test statistics, which is compared to the study statistics to help establish significance.

Common inferential statistics

Comparison tests: Comparison tests look for differences among group means. They can be used to test the effect of a categorical variable on the mean value of some other characteristic.

T-tests are used when comparing the means of precisely two groups (e.g., the average heights of men and women). ANOVA and MANOVA tests are used when comparing the means of more than two groups (e.g., the average heights of children, teenagers, and adults).

• T-tests (compares differences in two groups) – either paired t-test (example: What is the effect of two different test prep programs on the average exam scores for students from the same class?) or independent t-test (example: What is the difference in average exam scores for students from two different schools?)
• Analysis of variance (ANOVA, which compares differences in three or more groups) (example: What is the difference in average pain levels among post-surgical patients given three different painkillers?) or MANOVA (compares differences in three or more groups, and 2 or more outcomes) (example: What is the effect of flower species on petal length, petal width, and stem length?)

Correlation tests: Correlation tests check whether variables are related without hypothesizing a cause-and-effect relationship.

• Pearson r (measures the strength and direction of the relationship between two variables) (example: How are latitude and temperature related?)

Nonparametric tests: Non-parametric tests don’t make as many assumptions about the data, and are useful when one or more of the common statistical assumptions are violated. However, the inferences they make aren’t as strong as with parametric tests.

• chi-squared (X2) test (measures differences in proportions). Chi-square tests are often used to test hypotheses. The chi-square statistic compares the size of any discrepancies between the expected results and the actual results, given the size of the sample and the number of variables in the relationship. For example, the results of tossing a fair coin meet these criteria. We can apply a chi-square test to determine which type of candy is most popular and make sure that our shelves are well stocked. Or maybe you’re a scientist studying the offspring of cats to determine the likelihood of certain genetic traits being passed to a litter of kittens.

Statistical Significance Versus Clinical Significance

Finally, when it comes to statistical significance in hypothesis testing, the normal probability value in nursing is <0.05. A p-value (probability) is a statistical measurement used to validate a hypothesis against measured data in the study. Meaning, it measures the likelihood that the results were actually observed due to the intervention, or if the results were just due by chance. The p-value, in measuring the probability of obtaining the observed results, assumes the null hypothesis is true.

The lower the p-value, the greater the statistical significance of the observed difference.

In the example earlier about our diabetic patients receiving online diet education, let’s say we had p = 0.05. Would that be a statistically significant result?

If you answered yes, you are correct!

What if our result was p = 0.8?

Not significant. Good job!

That’s pretty straightforward, right? Below 0.05, significant. Over 0.05 not significant.

Could we have significance clinically even if we do not have statistically significant results? Yes. Let’s explore this a bit.

Statistical hypothesis testing provides little information for interpretation purposes. It’s pretty mathematical and we can still get it wrong. Additionally, attaining statistical significance does not really state whether a finding is clinically meaningful. With a large enough sample, even a small very tiny relationship may be statistically significant. But, clinical significance is the practical importance of research. Meaning, we need to ask what the palpable effects may be on the lives of patients or healthcare decisions.

Remember, hypothesis testing cannot prove. It also cannot tell us much other than “yeah, it’s probably likely that there would be some change with this intervention”. Hypothesis testing tells us the likelihood that the outcome was due to an intervention or influence and not just by chance. Also, as nurses and clinicians, we are not concerned with a group of people – we are concerned at the individual, holistic level. The goal of evidence-based practice is to use the best evidence for decisions about specific individual needs.