51 8.5 The Kinetic-Molecular Theory

Learning Objectives

By the end of this section, you will be able to:

  • State the postulates of the kinetic-molecular theory
  • Use this theory’s postulates to explain the gas laws

The gas laws that we have seen to this point, as well as the ideal gas equation, are empirical, that is, they have been derived from experimental observations. The mathematical forms of these laws closely describe the macroscopic behavior of most gases at pressures less than about 1 or 2 atm. Although the gas laws describe relationships that have been verified by many experiments, they do not tell us why gases follow these relationships.

The kinetic molecular theory (KMT) is a simple microscopic model that effectively explains the gas laws described in previous modules of this chapter. This theory is based on the following five postulates described here. (Note: The term “molecule” will be used to refer to the individual chemical species that compose the gas, although some gases are composed of atomic species, for example, the noble gases.)

  1. Gases are composed of molecules that are in continuous motion, travelling in straight lines and changing direction only when they collide with other molecules or with the walls of a container.
  2. The molecules composing the gas are negligibly small compared to the distances between them.
  3. The pressure exerted by a gas in a container results from collisions between the gas molecules and the container walls.
  4. Gas molecules exert no attractive or repulsive forces on each other or the container walls; therefore, their collisions are elastic (do not involve a loss of energy).
  5. The average kinetic energy of the gas molecules is proportional to the kelvin temperature of the gas.

The test of the KMT and its postulates is its ability to explain and describe the behavior of a gas. The various gas laws can be derived from the assumptions of the KMT, which have led chemists to believe that the assumptions of the theory accurately represent the properties of gas molecules. We will first look at the individual gas laws (Boyle’s, Charles’s, Amontons’s, Avogadro’s, and Dalton’s laws) conceptually to see how the KMT explains them. Then, we will more carefully consider the relationships between molecular masses, speeds, and kinetic energies with temperature, and explain Graham’s law.

The Kinetic-Molecular Theory Explains the Behavior of Gases, Part I

Recalling that gas pressure is exerted by rapidly moving gas molecules and depends directly on the number of molecules hitting a unit area of the wall per unit of time, we see that the KMT conceptually explains the behavior of a gas as follows:

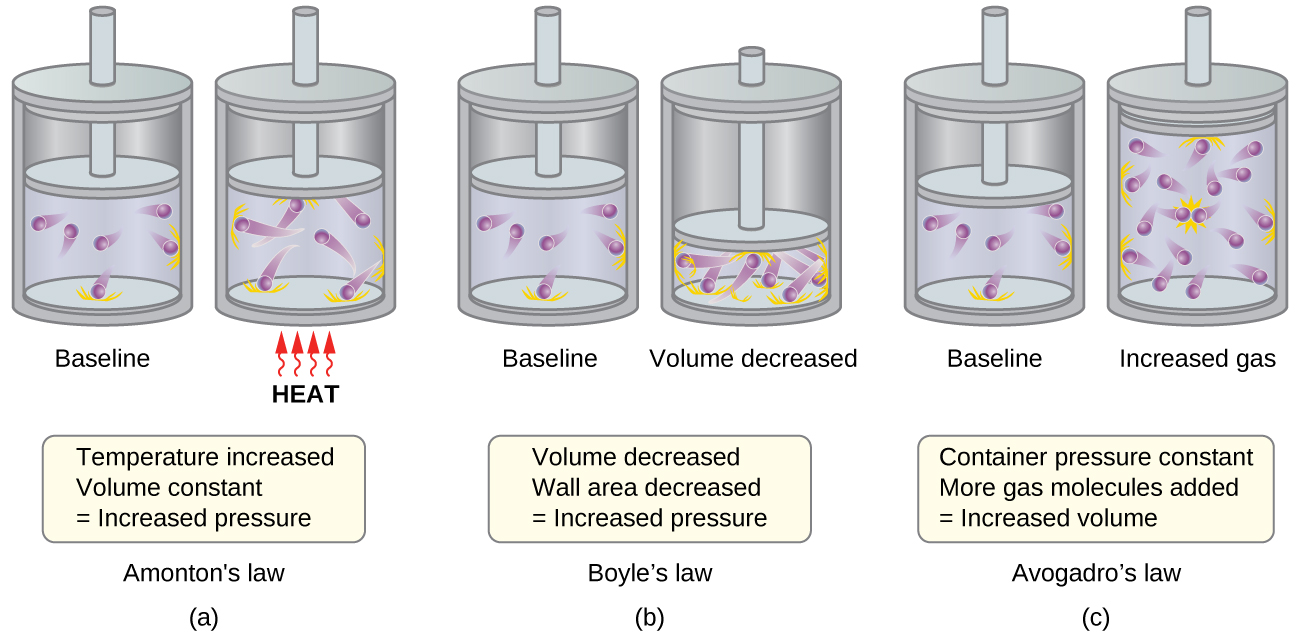
  • Amontons’s law. If the temperature is increased, the average speed and kinetic energy of the gas molecules increase. If the volume is held constant, the increased speed of the gas molecules results in more frequent and more forceful collisions with the walls of the container, therefore increasing the pressure (Figure 1).
  • Charles’s law. If the temperature of a gas is increased, a constant pressure may be maintained only if the volume occupied by the gas increases. This will result in greater average distances traveled by the molecules to reach the container walls, as well as increased wall surface area. These conditions will decrease the both the frequency of molecule-wall collisions and the number of collisions per unit area, the combined effects of which balance the effect of increased collision forces due to the greater kinetic energy at the higher temperature.
  • Boyle’s law. If the gas volume is decreased, the container wall area decreases and the molecule-wall collision frequency increases, both of which increase the pressure exerted by the gas (Figure 1).
  • Avogadro’s law. At constant pressure and temperature, the frequency and force of molecule-wall collisions are constant. Under such conditions, increasing the number of gaseous molecules will require a proportional increase in the container volume in order to yield a decrease in the number of collisions per unit area to compensate for the increased frequency of collisions (Figure 1).
  • Dalton’s Law. Because of the large distances between them, the molecules of one gas in a mixture bombard the container walls with the same frequency whether other gases are present or not, and the total pressure of a gas mixture equals the sum of the (partial) pressures of the individual gases.
This figure shows 3 pairs of pistons and cylinders. In a, which is labeled, “Charles’s Law,” the piston is positioned for the first cylinder so that just over half of the available volume contains 6 purple spheres with trails behind them. The trails indicate movement. Orange dashes extend from the interior surface of the cylinder where the spheres have collided. This cylinder is labeled, “Baseline.” In the second cylinder, the piston is in the same position, and the label, “Heat” is indicated in red capitalized text. Four red arrows with wavy stems are pointing upward to the base of the cylinder. The six purple spheres have longer trails behind them and the number of orange dashes indicating points of collision with the container walls has increased. A rectangle beneath the diagram states, “Temperature increased, Volume constant equals Increased pressure.” In b, which is labeled, “Boyle’s Law,” the first, baseline cylinder shown is identical to the first cylinder in a. In the second cylinder, the piston has been moved, decreasing the volume available to the 6 purple spheres to half of the initial volume. The six purple spheres have longer trails behind them and the number of orange dashes indicating points of collision with the container walls has increased. This second cylinder is labeled, “Volume decreased.” A rectangle beneath the diagram states, “Volume decreased, Wall area decreased equals Increased pressure.” In c, which is labeled “Avogadro’s Law,” the first, baseline cylinder shown is identical to the first cylinder in a. In the second cylinder, the number of purple spheres has changed from 6 to 12 and volume has doubled. This second cylinder is labeled “Increased gas.” A rectangle beneath the diagram states, “At constant pressure, More gas molecules added equals Increased volume.”
Figure 1. (a) When gas temperature increases, gas pressure increases due to increased force and frequency of molecular collisions. (b) When volume decreases, gas pressure increases due to increased frequency of molecular collisions. (c) When the amount of gas increases at a constant pressure, volume increases to yield a constant number of collisions per unit wall area per unit time.

Molecular Velocities and Kinetic Energy

The previous discussion showed that the KMT qualitatively explains the behaviors described by the various gas laws. The postulates of this theory may be applied in a more quantitative fashion to derive these individual laws. To do this, we must first look at velocities and kinetic energies of gas molecules, and the temperature of a gas sample.

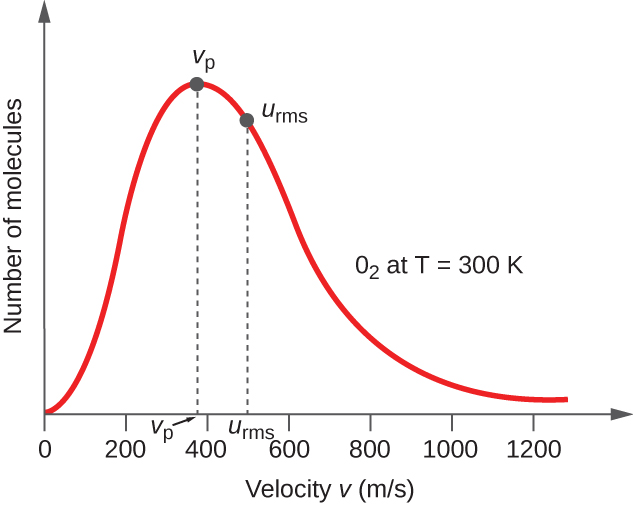
In a gas sample, individual molecules have widely varying speeds; however, because of the vast number of molecules and collisions involved, the molecular speed distribution and average speed are constant. This molecular speed distribution is known as a Maxwell-Boltzmann distribution, and it depicts the relative numbers of molecules in a bulk sample of gas that possesses a given speed (Figure 2).

A graph is shown. The horizontal axis is labeled, “Velocity v ( m divided by s ).” This axis is marked by increments of 20 beginning at 0 and extending up to 120. The vertical axis is labeled, “Fraction of molecules.” A positively or right-skewed curve is shown in red which begins at the origin and approaches the horizontal axis around 120 m per s. At the peak of the curve, a point is indicated with a black dot and is labeled, “v subscript p.” A vertical dashed line extends from this point to the horizontal axis at which point the intersection is labeled, “v subscript p.” Slightly to the right of the peak a second black dot is placed on the curve. This point is labeled, “v subscript r m s.” A vertical dashed line extends from this point to the horizontal axis at which point the intersection is labeled, “v subscript r m s.” The label, “O subscript 2 at T equals 300 K” appears in the open space to the right of the curve.
Figure 2. The molecular speed distribution for oxygen gas at 300 K is shown here. Very few molecules move at either very low or very high speeds. The number of molecules with intermediate speeds increases rapidly up to a maximum, which is the most probable speed, then drops off rapidly. Note that the most probable speed, νp, is a little less than 400 m/s, while the root mean square speed, urms, is closer to 500 m/s.

The kinetic energy (KE) of a particle of mass (m) and speed (u) is given by:

[latex]\text{KE} = \frac{1}{2}mu^2[/latex]

Expressing mass in kilograms and speed in meters per second will yield energy values in units of joules (J = kg m2 s–2). To deal with a large number of gas molecules, we use averages for both speed and kinetic energy. In the KMT, the root mean square velocity of a particle, urms, is defined as the square root of the average of the squares of the velocities with n = the number of particles:

[latex]u_{\text{rms}} = \sqrt{\overline{u^2}} = \sqrt{\frac{u^2_1 + u^2_2 + u^2_3 + u^2_4 + \cdots}{n}}[/latex]

The average kinetic energy, KEavg, is then equal to:

[latex]\text{KE}_{\text{avg}} = \frac{1}{2}mu^2_{\text{rms}}[/latex]

The KEavg of a collection of gas molecules is also directly proportional to the temperature of the gas and may be described by the equation:

[latex]\text{KE}_{\text{avg}} = \frac{3}{2}RT[/latex]

where R is the gas constant and T is the kelvin temperature. When used in this equation, the appropriate form of the gas constant is 8.314 J/K (8.314 kg m2s–2K–1). These two separate equations for KEavg may be combined and rearranged to yield a relation between molecular speed and temperature:

[latex]\frac{1}{2} mu^2_{\text{rms}} = \frac{3}{2}RT[/latex]
which simplifies to:
[latex]u_{\text{rms}} = \sqrt{\frac{3RT}{m}}[/latex]

Example 1

Calculation of urms
Calculate the root-mean-square velocity for a nitrogen molecule at 30 °C.

Solution
Convert the temperature into Kelvin:

[latex]30 \;^{\circ}\text{C} + 273 = 303 \;\text{K}[/latex]

Determine the mass of a nitrogen molecule in kilograms:

[latex]\frac{28.0 \;\rule[0.3ex]{0.5em}{0.1ex}\hspace{-0.4em}\text{g}}{1 \;\text{mol}} \times \frac{1 \;\text{kg}}{1000 \;\rule[0.3ex]{0.5em}{0.1ex}\hspace{-0.4em}\text{g}} = 0.028 \;\text{kg/mol}[/latex]

Replace the variables and constants in the root-mean-square velocity equation, replacing Joules with the equivalent kg m2s–2:

[latex]u_{\text{rms}} = \sqrt{\frac{3RT}{m}}\\[0.5em][/latex]
[latex]u_{\text{rms}} = \sqrt{\frac{3(8.314 \;\text{J/mol K})(303 \;\text{K})}{(0.028 \;\text{kg/mol})}} = \sqrt{2.70 \times 10^5 \;\text{m}^2\text{s}^{-2}} = 519 \;\text{m/s}\\[0.5em][/latex]

 

Check Your Learning
Calculate the root-mean-square velocity for an oxygen molecule at –23 °C.

Answer:

441 m/s

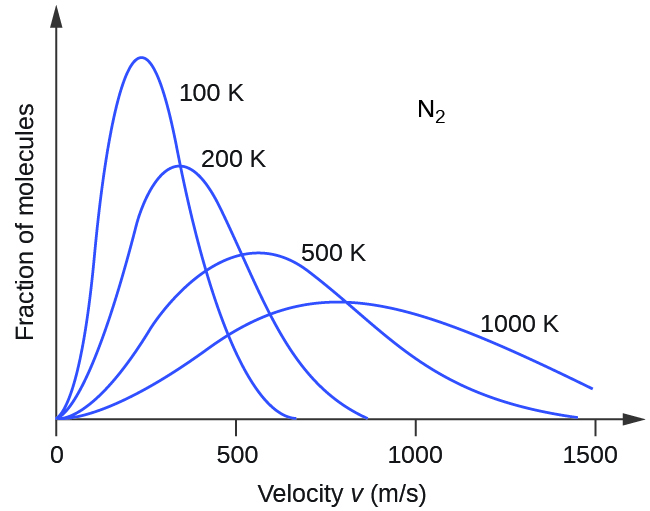
If the temperature of a gas increases, its KEavg increases, more molecules have higher speeds and fewer molecules have lower speeds, and the distribution shifts toward higher speeds overall, that is, to the right. If temperature decreases, KEavg decreases, more molecules have lower speeds and fewer molecules have higher speeds, and the distribution shifts toward lower speeds overall, that is, to the left. This behavior is illustrated for nitrogen gas in Figure 3.

A graph with four positively or right-skewed curves of varying heights is shown. The horizontal axis is labeled, “Velocity v ( m divided by s ).” This axis is marked by increments of 500 beginning at 0 and extending up to 1500. The vertical axis is labeled, “Fraction of molecules.” The label, “N subscript 2,” appears in the open space in the upper right area of the graph. The tallest and narrowest of these curves is labeled, “100 K.” Its right end appears to touch the horizontal axis around 700 m per s. It is followed by a slightly wider curve which is labeled, “200 K,” that is about three quarters of the height of the initial curve. Its right end appears to touch the horizontal axis around 850 m per s. The third curve is significantly wider and only about half the height of the initial curve. It is labeled, “500 K.” Its right end appears to touch the horizontal axis around 1450 m per s. The final curve is only about one third the height of the initial curve. It is much wider than the others, so much so that its right end has not yet reached the horizontal axis. This curve is labeled, “1000 K.”
Figure 3. The molecular speed distribution for nitrogen gas (N2) shifts to the right and flattens as the temperature increases; it shifts to the left and heightens as the temperature decreases.

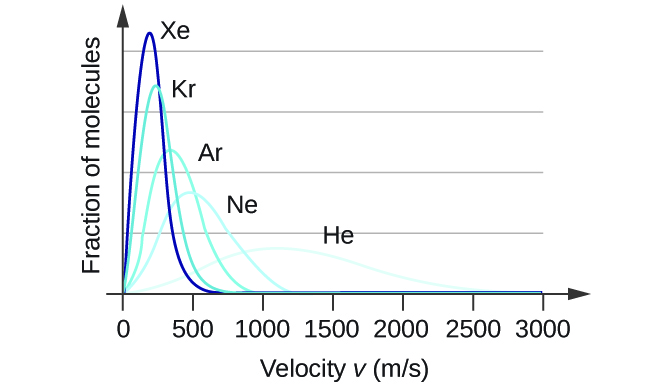
At a given temperature, all gases have the same KEavg for their molecules. Gases composed of lighter molecules have more high-speed particles and a higher urms, with a speed distribution that peaks at relatively higher velocities. Gases consisting of heavier molecules have more low-speed particles, a lower urms, and a speed distribution that peaks at relatively lower velocities. This trend is demonstrated by the data for a series of noble gases shown in Figure 4.

A graph is shown with four positively or right-skewed curves of varying heights. The horizontal axis is labeled, “Velocity v ( m divided by s ).” This axis is marked by increments of 500 beginning at 0 and extending up to 3000. The vertical axis is labeled, “Fraction of molecules.” The tallest and narrowest of these curves is labeled, “X e.” Its right end appears to touch the horizontal axis around 600 m per s. It is followed by a slightly wider curve which is labeled, “A r,” that is about half the height of the initial curve. Its right end appears to touch the horizontal axis around 900 m per s. The third curve is significantly wider and just over a third of the height of the initial curve. It is labeled, “N e.” Its right end appears to touch the horizontal axis around 1200 m per s. The final curve is only about one fourth the height of the initial curve. It is much wider than the others, so much so that its right reaches the horizontal axis around 2500 m per s. This curve is labeled, “H e.”
Figure 4. Molecular velocity is directly related to molecular mass. At a given temperature, lighter molecules move faster on average than heavier molecules.

 

The gas simulator may be used to examine the effect of temperature on molecular velocities. Examine the simulator’s “energy histograms” (molecular speed distributions) and “species information” (which gives average speed values) for molecules of different masses at various temperatures.

The Kinetic-Molecular Theory Explains the Behavior of Gases, Part II

According to Graham’s law, the molecules of a gas are in rapid motion and the molecules themselves are small. The average distance between the molecules of a gas is large compared to the size of the molecules. As a consequence, gas molecules can move past each other easily and diffuse at relatively fast rates.

The rate of effusion of a gas depends directly on the (average) speed of its molecules:

[latex]\text{effusion rate} \propto u_{\text{rms}}[/latex]

Using this relation, and the equation relating molecular speed to mass, Graham’s law may be easily derived as shown here:

[latex]u_{\text{rms}} = \sqrt{\frac{3RT}{m}}\\[0.5em][/latex]
[latex]m = \frac{3RT}{u^2_{\text{rms}}} = \frac{3RT}{\overline{u}^2}\\[0.5em][/latex]
[latex]\frac{\text{effusion rate of A}}{\text{effusion rate of B}} = \frac{u_{\text{rms A}}}{u_{\text{rms B}}} = \frac{\sqrt{\frac{3RT}{m_\text{A}}}}{\sqrt{\frac{3RT}{m_\text{B}}}} = \sqrt{\frac{m_{\text{B}}}{m_{\text{A}}}}\\[0.5em][/latex]

The ratio of the rates of effusion is thus derived to be inversely proportional to the ratio of the square roots of their masses. This is the same relation observed experimentally and expressed as Graham’s law.

Key Concepts and Summary

The kinetic molecular theory is a simple but very effective model that effectively explains ideal gas behavior. The theory assumes that gases consist of widely separated molecules of negligible volume that are in constant motion, colliding elastically with one another and the walls of their container with average velocities determined by their absolute temperatures. The individual molecules of a gas exhibit a range of velocities, the distribution of these velocities being dependent on the temperature of the gas and the mass of its molecules.

Key Equations

  • [latex]u_{\text{rms}} = \sqrt{\overline{u^2}} = \sqrt{\frac{u^2_1 + u^2_2 + u^2_3 + u^2_4 + \cdots}{n}}\\[0.5em][/latex]
  • [latex]\text{KE}_{\text{avg}} = \frac{3}{2}RT\\[0.5em][/latex]
  • [latex]u_{\text{rms}} = \sqrt{\frac{3RT}{m}}[/latex]

Chemistry End of Chapter Exercises

  1. Using the postulates of the kinetic molecular theory, explain why a gas uniformly fills a container of any shape.
  2. Can the speed of a given molecule in a gas double at constant temperature? Explain your answer.
  3. Describe what happens to the average kinetic energy of ideal gas molecules when the conditions are changed as follows:

    (a) The pressure of the gas is increased by reducing the volume at constant temperature.

    (b) The pressure of the gas is increased by increasing the temperature at constant volume.

    (c) The average velocity of the molecules is increased by a factor of 2.

  4. The distribution of molecular velocities in a sample of helium is shown in Figure 4. If the sample is cooled, will the distribution of velocities look more like that of H2 or of H2O? Explain your answer.
  5. What is the ratio of the average kinetic energy of a SO2 molecule to that of an O2 molecule in a mixture of two gases? What is the ratio of the root mean square speeds, urms, of the two gases?
  6. A 1-L sample of CO initially at STP is heated to 546 °C, and its volume is increased to 2 L.

    (a) What effect do these changes have on the number of collisions of the molecules of the gas per unit area of the container wall?

    (b) What is the effect on the average kinetic energy of the molecules?

    (c) What is the effect on the root mean square speed of the molecules?

  7. The root mean square speed of H2 molecules at 25 °C is about 1.6 km/s. What is the root mean square speed of a N2 molecule at 25 °C?
  8. Answer the following questions:

    (a) Is the pressure of the gas in the hot air balloon shown at the opening of this chapter greater than, less than, or equal to that of the atmosphere outside the balloon?

    (b) Is the density of the gas in the hot air balloon shown at the opening of this chapter greater than, less than, or equal to that of the atmosphere outside the balloon?

    (c) At a pressure of 1 atm and a temperature of 20 °C, dry air has a density of 1.2256 g/L. What is the (average) molar mass of dry air?

    (d) The average temperature of the gas in a hot air balloon is 1.30 × 102 °F. Calculate its density, assuming the molar mass equals that of dry air.

    (e) The lifting capacity of a hot air balloon is equal to the difference in the mass of the cool air displaced by the balloon and the mass of the gas in the balloon. What is the difference in the mass of 1.00 L of the cool air in part (c) and the hot air in part (d)?

    (f) An average balloon has a diameter of 60 feet and a volume of 1.1 × 105 ft3. What is the lifting power of such a balloon? If the weight of the balloon and its rigging is 500 pounds, what is its capacity for carrying passengers and cargo?

    (g) A balloon carries 40.0 gallons of liquid propane (density 0.5005 g/L). What volume of CO2 and H2O gas is produced by the combustion of this propane?

    (h) A balloon flight can last about 90 minutes. If all of the fuel is burned during this time, what is the approximate rate of heat loss (in kJ/min) from the hot air in the bag during the flight?

  9. Show that the ratio of the rate of diffusion of Gas 1 to the rate of diffusion of Gas 2, [latex]\frac{R_1}{R_2}[/latex], is the same at 0 °C and 100 °C.

Glossary

kinetic molecular theory
theory based on simple principles and assumptions that effectively explains ideal gas behavior
root mean square velocity (urms)
measure of average velocity for a group of particles calculated as the square root of the average squared velocity

Solutions

2. Yes. At any given instant, there are a range of values of molecular speeds in a sample of gas. Any single molecule can speed up or slow down as it collides with other molecules. The average velocity of all the molecules is constant at constant temperature.

4. H2O. Cooling slows the velocities of the He atoms, causing them to behave as though they were heavier.

6. (a) The number of collisions per unit area of the container wall is constant. (b) The average kinetic energy doubles. (c) The root mean square speed increases to [latex]\sqrt{2}[/latex] times its initial value; urms is proportional to [latex]\sqrt{\text{KE}_{\text{avg}}}[/latex].

8. (a) equal; (b) less than; (c) 29.48 g mol−1; (d) 1.0966 g L−1; (e) 0.129 g/L; (f) 4.01 × 105 g; net lifting capacity = 384 lb; (g) 270 L; (h) 39.1 kJ min−1

License

Icon for the Creative Commons Attribution 4.0 International License

General Chemistry 1 & 2 Copyright © 2016 by Rice University is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book