12.1 Optimal Foraging Theory
Every animal must eat, which means every animal must search for and collect resources. Feeding behaviors that maximize energy gain and minimize energy expenditure are called optimal foraging behaviors, or more formally Optimal Foraging Theory (OFT), and these are favored by natural section. As a result, foraging strategies can actually drive our behavior in a myriad of ways.
Optimal Foraging Theory can be demonstrated as the following:
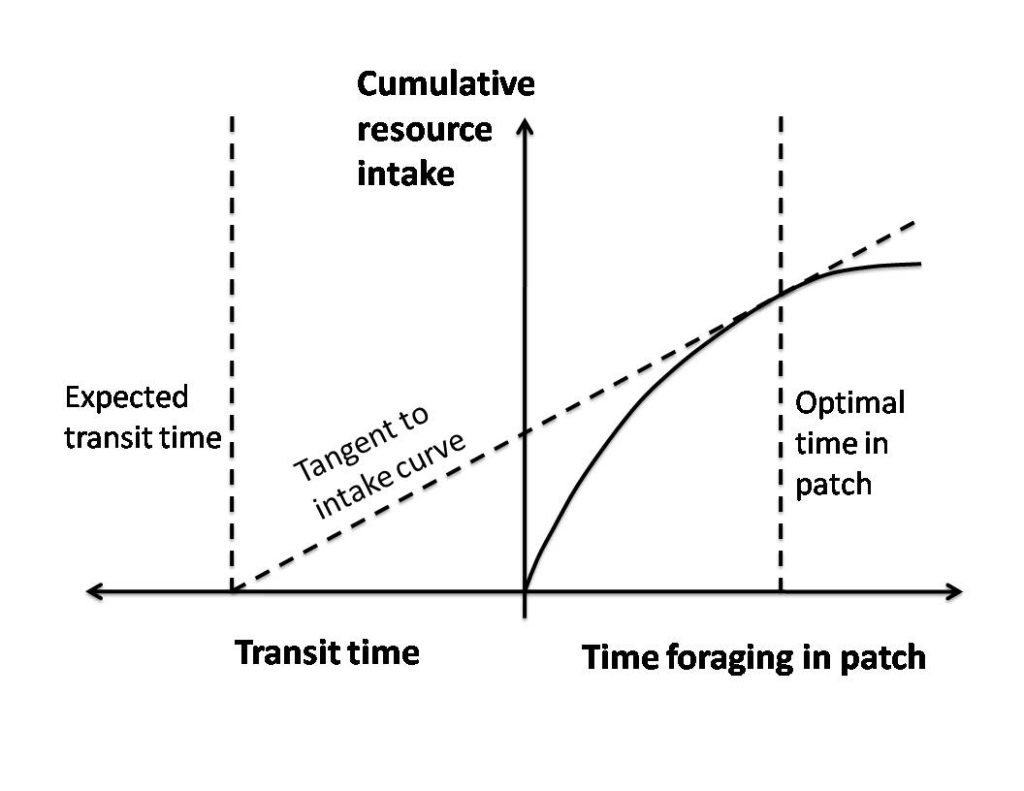
The Marginal Value Theorem is used by biologists and anthropologists to demonstrate the cost-benefit analysis inherent in Optimal Foraging. In essence, OFT can be viewed as the equation “net energy gain / unit of time,” where the total should be a positive number.
For example, let’s say a person is going to forage for berries in the spring. The unit of time includes time spent traveling to a berry patch, time spent collecting berries, and time to return, prepare, or eat the food. This is generally represented in calories burned or minutes.
The energy gained is based upon the caloric content of food acquired. This is a total number, so the berries along with any additional resources (perhaps a lemonade taken along from home) are included. This is represented as total calories gained/ingested.
According to the USDA, a large strawberry contains six (6) calories. If our forager gathers 20 large strawberries, they have gained approximately 120 calories. If they did take along that lemonade, we can add the 150 calories (for a 16 oz Minute Maid Lemonade). This means their total calories obtained is 270 calories.
The average, healthy person can burn approximately 200 calories per hour for a slow, leisurely walk. But foraging also includes time stopped while collecting the food items. Let’s assume those stops add to approximately 50 calories not burned. As a result, a one-hour foraging session burns about 150 calories.
We can now calculate the foraging returns for our berry forager.
energy gained (270 cal) / energy spent (150 cal) = 1.8
This means our berry forager obtained 1.8 times the total calories spent foraging – a success. Of course, without that lemonade, they would have had a 30-calorie deficit.
This is a simplified example, based upon one person’s energy needs and expenditures. It can certainly get more complicated. Mothers who are also feeding young children, men who are hunting for a full camp, and other expectations for sharing can increase the number of calories needed. This is because the actual energy gained will be divided by multiple mouths – though not necessarily via equal distribution.

