3.4 Hardy-Weinberg Equilibrium

In the early twentieth century, Godfrey Hardy (1877-1947) and Wilhelm Weinberg (1862-1937) stated the principle of equilibrium to describe a population’s genetic makeup. Known as the Hardy-Weinberg Equilibrium, this principle states that a population’s allele and genotype frequencies are inherently stable — unless evolutionary force is acting upon the population, neither the allele nor the genotypic frequencies would change. This provided mathematical structure to Darwin’s postulates and created a way for scientists to track population change.

Different alleles represent different variables in their mathematical model. The variable p, for example, often represents the frequency of a particular allele, say Y for the trait of yellow in Mendel’s peas, while the variable q represents the frequency of y alleles that confer the color green. If these are the only two possible alleles for a given locus in the population, p + q = 1. In other words, all the p alleles and all the q alleles comprise all the alleles for that locus in the population.

In the above scenario, an individual pea plant could be pp (YY), and thus produce yellow peas; pq (Yy), also yellow; or qq (yy), and thus produce green peas (Figure 3.6). In other words, the frequency of pp individuals is simply p2; the frequency of pq individuals is 2pq; and the frequency of qq individuals is q2. Again, if p and q are the only two possible alleles for a given trait in the population, these genotypes frequencies will sum to one: p2 + 2pq + q2 = 1.

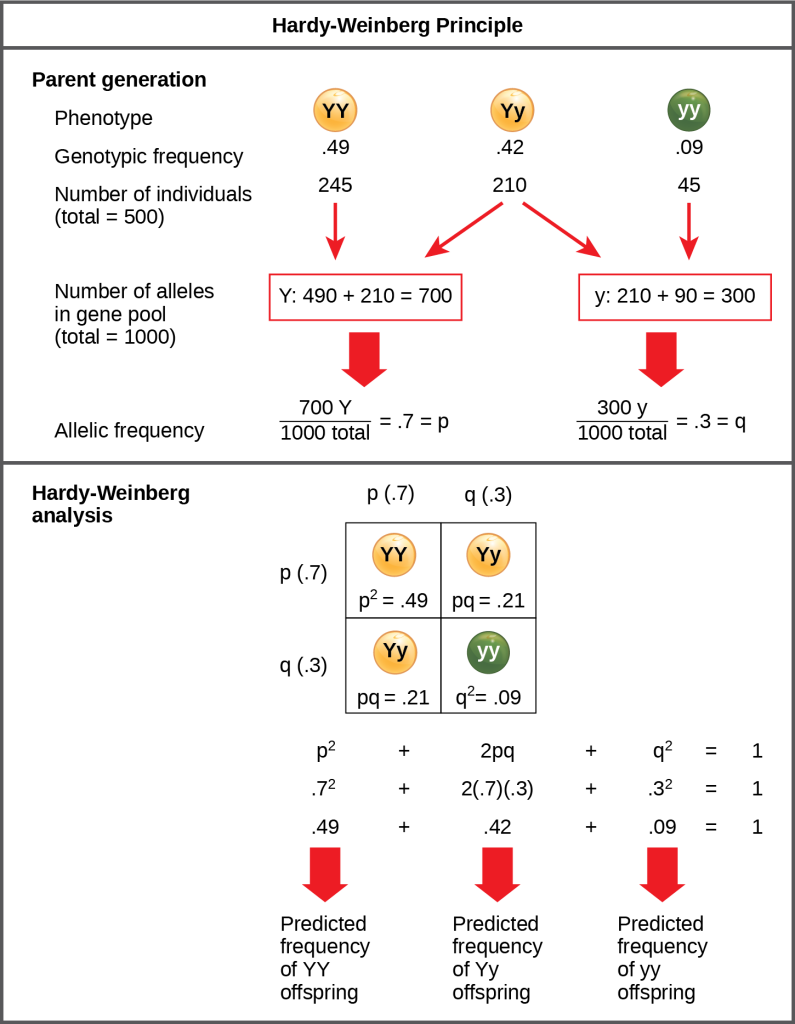
In theory, if a population is at equilibrium — that is, there are no evolutionary forces acting upon it — generation after generation would have the same gene pool and genetic structure, and these equations would hold true all the time. Of course, like Darwin and Wallace, Hardy and Weinberg recognized that no natural population is immune to evolution. Populations in nature are constantly changing in genetic makeup due to genetic drift, mutation, possibly migration, and selection. As a result, the only way to determine the exact distribution of phenotypes in a population is to go out and count them. However, the Hardy -Weinberg principle gives scientists a mathematical baseline of a non-evolving population to which they can compare evolving populations and thereby infer what evolutionary forces might be at play. If the frequencies of alleles or genotypes deviate from the value expected from the Hardy -Weinberg equation, then the population is evolving.

Below is a great video explaining the Hardy-Weinberg equation.